1619: 弦截法求方程的根

用弦截法求方程的根，方程如下：

算法：

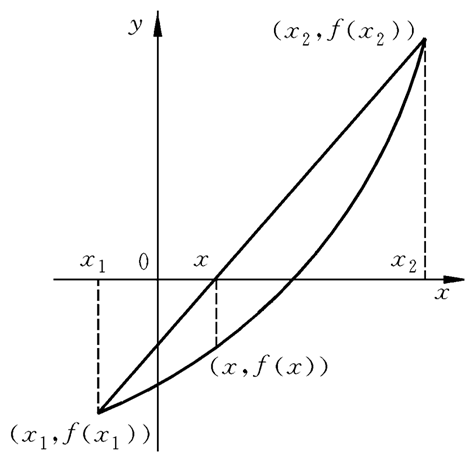
1、取两个不同点x1,x2,如果f(x1)和f(x2)符号相反,则(x1,x2)区间内必有一个根。如果f(x1)与f(x2)同符号,则应改变x1,x2,直到f(x1)、f(x2)异号为止。

2、连接(x1,f(x1))和(x2,f(x2))两点,此线(即弦)交x轴于x。X点坐标可以由下式求出：

X=(x1f(x2)-x2f(x1))/(f(x2)-f(x1))

再从x求出f(x)

3、若f(x)与f(x1)同符号,则根必在(x,x2)区间内,此时将x作为新的x1。如果f(x)与f(x2)同符号,则表示根在(x1,x)区间内,将x作为新的x2。

4、重复步骤(2)和(3),直到｜f(x)｜＜ε为止, ε为一个很小的数, 例如 10^-6. 此时认为 f(x)≈0。